Remove terrible bus routes (find an algorithm)
Problem statement
You are taking the bus from A to B, sometime today. You have a list of all possible trips, with a trip being represented as the tuple (leave_time, arrive_time). The time you leave A, and the time you get to B, respectively. Both times are represented as integers.
You don’t care about what the route looks like, so even really bad choices are included. There may be arbitrarily many ways of getting from A to B, some worse than others.
Turns out many of the trips are so bad that you would never want to take them. Therefore you would want to tidy up the list. Duplicates should be removed, and any trip that is objectively worse than another trip should be removed.
A trip X is objectively worse than another trip Y if X.leave_time <= Y.leave_time && X.arrive_time >= Y.arrive_time. Basically if you can leave from A later, and still arrive at B earlier, there is no point in ever taking trip X.
Given the list, write a function that returns a sorted and tidied up list.
Input
Input is read from a file or the console.
The first line contains an integer N (1 < N <= 1e5), the number of trips given.
The following N lines contain two integers leave_time and arrive_time (1 <= leave_time <= arrive_time <= 1e6), denoting a trip in the list.
Output
Output is printed out in the console or to a file.
One the first line, print the number of trips in the tidied list M.
Followed by M lines, with the integers arrive_time and leave_time for each trip in sorted order.
Sample input 1
8
15 30
12 28
15 32
8 42
15 30
10 30
25 40
28 38
Expected output:
3
12 28
15 30
28 38
Explanation
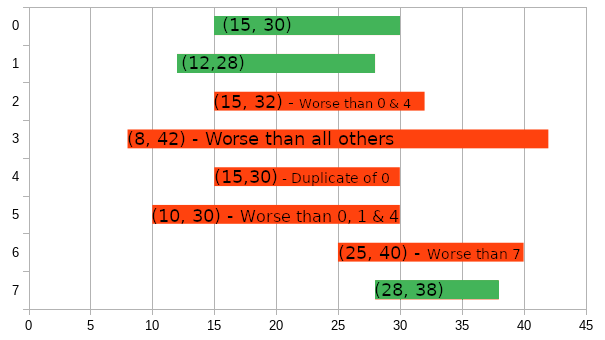
Each interval represents a possible trip. The (leave_time, arrival_time) tuple is written on the box. If the trip is objectively worse than another, the box is red, with an explanation written on it.
The routes that are left (green) are then sorted and printed.
Sample input 2
30
23 59
17 82
85 90
76 95
44 87
78 78
51 88
73 80
10 31
84 95
38 56
92 96
66 71
77 98
94 98
94 98
91 99
83 98
91 94
63 77
33 69
3 63
13 54
37 80
27 40
52 92
90 98
41 91
11 96
16 65
Expected output:
9
10 31
27 40
38 56
66 71
78 78
85 90
91 94
92 96
94 98